scikit机器学习
sklearn (scikit-learn) 是基于 Python 语言的机器学习工具
- 简单高效的数据挖掘和数据分析工具
- 可供大家在各种环境中重复使用
- 建立在 NumPy ,SciPy 和 matplotlib 上
- 开源,可商业使用 - BSD许可证
[TOC]
classification
监督学习
线性模型
当我们需要预测的 target_value期望是一个线性拟合的时候,数学公式表达为:
$$
\hat{y}(w, x) = w_0 + w_1 x_1 + … + w_p x_p
$$
其中 向量 w 表示 coef_ ,这大概是斜率的意思
w_0表示 intercept 表示截距
线性回归的含义是用一个线性函数去拟合向量w,使得预测值和真实值的残差平方和最小
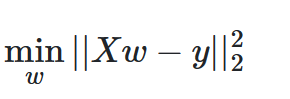
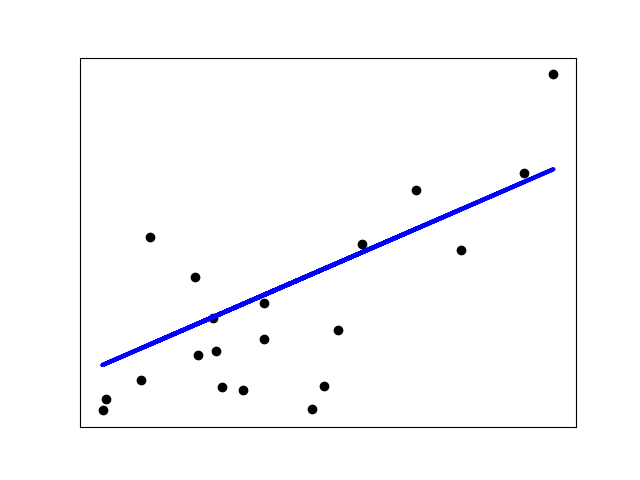
线性回归会用 fit函数去接收数组X,Y ,并且会自动计算出斜率以及截距
以下是示例代码:
1 | from sklearn import linear_model |
注意:最小二乘法来计算回归系数的时候非常依赖变量(feature)之间的独立性
当features之间是相关的,并且X的矩阵大概率也是线性相关的,在这种情况下,
通常会发生:
我们的最小二乘法拟合函数会对随机误差非常敏感,从而产生很大的方差
所以变量之间尽量是相互独立的,避免引发多重共线性
官方代码样例见github仓库
岭回归与分类(Ridge regression and classfication)
类似于最小二乘法,岭回归增加了对于回归系数的惩罚
具体公式是这样的:
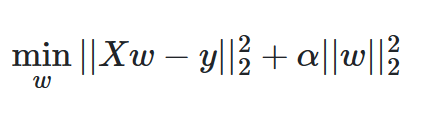
$$
\alpha 控制着收缩的变化程度,当\alpha越大的时候,收缩的程度越大,因此回归系数会变得对共线性具有鲁棒性
$$
同时我也查阅了岭回归出现的原因
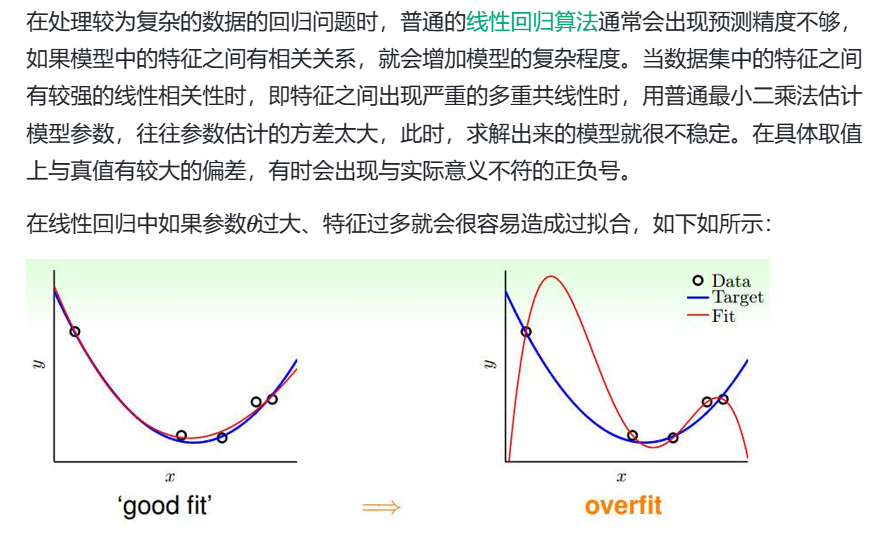
对于多重共线性的数据,其loss函数求偏导后分母近似奇异矩阵,解得的ω \omegaω误差大;我们对loss函数加上ω \omegaω的2范数,使得求偏导后分母变为满秩矩阵,和普通最小二乘相类似,可以很好的计算出相对稳定的结果。
岭分类
本质上还是将分类问题转化为回归问题,然后用岭回归去解决
官方文档中提到: The RidgeClassifier can be significantly faster than e.g. LogisticRegression with a high number of classes because it can compute the projection matrixonly once.
该分类器有时被称为具有线性内核的最小二乘支持向量机
岭回归的优势与劣势
以岭回归为例,它为了解决一些普通最小二乘遇到的问题,对系数ω 的大小施加惩罚。
这样做虽然增强了稳定性,但是同时也牺牲了保真性(就是从我们所求的系数ω 并不是真正意义上向最优系数ω
Ridge回归在不抛弃任何一个变量的情况下,缩小了回归系数,使得模型相对而言比较的稳定,但这会使得模型的变量特别多,模型解释性差。
当然,既然存在这种方法,那么证明在处理这些问题的时候,Ridge Regression 能取得比普通最小二乘更好的性能。



